Here is an opinionated proposal, having no chance whatsoever of adoption, for how taxes ought to be levied on income. This post was originally scheduled for Income Tax Day here in the good old U.S.A., but I was having trouble with the algebra and then I was on vacation. So instead you get it for Canadian tax day. Everything is calculated in US dollars and compared to existing US systems, but I don’t see any great difficulty translating it to other countries.

Premises for this redesign:

• The existing tax code is way too damn complicated.
• It is the rules that need to be simplified, not the mathematics. In particular, the marginal tax rate does not need to be a step function just to simplify the arithmetic involved. You look that part up in a table anyway.
• All individuals’ take-home pay should increase monotonically with their gross income, regardless of any other factors.
• High levels of income inequality constitute a negative externality; income tax should therefore be Pigovian.
• Tax rates should not vary based on any categorization of income (e.g. interest and capital gains should be taxed at the same rate as wages). This principle by itself removes a great deal of the complexity, and a great deal of the perverse incentives in the current system as well.

Read on for concrete details of the proposal.

The first thing we do is institute an unconditional basic income. (Just to poke David Weber in the eye, let’s call it the Basic Living Stipend.) Every adult gets $B$ dollars every year, in monthly installments, unconditionally and untaxed. The value of $B$ is set by statute when the reforms go into effect and automatically adjusted for inflation thereafter. In this hypothetical I’m setting $B$ to $24,000 for concreteness; this is a nice round number—$2000 a month—that happens to be a little more than 200% of the (USA) Federal poverty line for a one-person household in 2014, according to http://familiesusa.org/product/federal-poverty-guidelines.

We also institute a unified national pension. It works hand in hand with the tax scheme, so I’ll explain that first and come back to this, but you need to know the pension exists. It differs from existing pensions in one important way: it starts paying immediately upon your having made any amount of contribution; there is no age or disability requirement. (It may not pay out very much, though, as I’ll explain below.) Income from the pension is not taxed either, but it raises your marginal tax rate as if it had been taxed. The combination of the BLS and the pension are intended to replace all existing government-administered pension plans (Social Security, the Railroad Retirement Board, etc.), disability benefits, unemployment insurance, etc.

All income from other sources is taxed according to the same formula. This tax replaces all income and payroll taxes collected by the IRS. There are no deductions, exemptions, credits, special categories, or anything else. Congress gets one and only one adjustment knob: the set point, $(s,r)$. A marginal tax rate of $r\%$ is charged on the $s$’th dollar of income above $B$. The marginal tax rate $M$ on the $i$’th dollar of income is

$$M = \begin{cases} \frac{r(B-i)}{r(s-i)-s} & \text{if}\:\: i > B\\\\ 0 & \text{otherwise} \end{cases}$$

and one’s after-tax income, $A$, if one earns $I$ dollars in total (of which $B$ are from the BLS and $P$ the pension), is

$$\begin{aligned}\displaystyle A = B + P + &\int_{B+P}^I 1-M(i)\;di\\\\ = B + P + &\frac{rB+(1-r)s}{r}\, \Bigl[ \ln\, \bigl(rI+(1-r)s\bigr) - \ln\, \bigl(rB+rP+(1-r)s\bigr) \Bigr] \end{aligned}$$

These functions look messy, and possibly I am out of my mind to even suggest them to such a pack of know-nothings as we have presently in Congress, but they have exactly the mathematical properties we want. $M$ is continuous, increases monotonically, and converges to 1 at positive infinity, but $A$ diverges at positive infinity, so there is no upper limit in principle on after-tax income. (As we shall see, though, in practice that next after-tax dollar gets very, very expensive past a certain point.) Also, the equations get a lot less messy if we substitute in numbers for some of the parameters. For instance, setting $B = 24000$, $s = 500000$, and $r = 40\%$ (corresponding to the blue line below) gives us $A = 24000 + P + 774000 \bigl( \ln\,(0.4I + 300000) - \ln\,(0.4P + 309600) \bigr)$ for the formula that taxpayers would actually have to wrestle with.

Below is a chart of the marginal tax rate and the after-tax income for several choices of $r$, with $s$ fixed to $500,000. For comparison, the jagged gray line is the real marginal tax rate for the USA for 2013 (for individuals under the age of 65, all income wages, taking the standard deduction and one exemption, with no other adjustments or credits—this is a gross oversimplification, but attempting to factor in things like the EITC and the AMT was too complicated for me; if someone wants to provide me with a more realistic comparison curve I am happy to update the chart). Do keep in mind that after the reform, everyone has at least $24,000 of yearly income. The x-axis in both charts, and the y-axis in the right-hand chart, are on a log₁₀ scale. Click to embiggen.

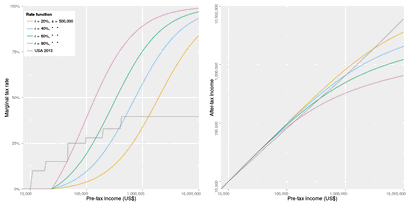
You can see that regardless of the choice of set point, this is likely to be a modest tax cut for people earning less than $100,000 a year, and a hefty tax hike for people earning more than that. That’s by design. It should be almost unheard of for anyone to earn more than $500,000 or so a year after taxes. This is what makes this a Pigovian correction to the negative externalities involved in high income inequality. (For instance, an expected consequence of this reform is that corporations will stop throwing money away on their executives.)

Now, remember that pension scheme? That’s automatically funded for each individual by the taxes they pay in. This obeys a similar formula to the taxation itself. There are two control points: the first dollar paid in taxes returns a pension of $p_0$ dollars per year, and the $s$’th dollar paid in taxes returns a pension of $p_r$ dollars per year, where $p_r < p_0 <1$. The marginal pension payout $p$ on the $t$’th dollar paid in taxes is

$$p = \frac{p_0 p_r (1-s)}{p_0 - p_rs - (p_0 - p_r)t}$$

and the cumulative payout on $T$ dollars paid in is

$$\begin{aligned} P &= \int_1^T p(t)\,dt\\\\ &= \frac{p_0 p_r (s-1)}{p_0 - p_r} \Bigl[ \ln\,\bigl( p_r s - p_0 + (p_0 - p_r)T\bigr) -\ln\, p_r (s - 1) \Bigr] \end{aligned}$$

The amount paid into the pension scheme accumulates year over year, but every year it’s multiplied by a decay factor, $d < 1$. The next chart shows three hypothetical yearly pretax incomes (not including BLS or pension), pension accumulation, and the resulting after-tax income, all as a function of time, for plausible choices of the parameters: $s = 500000,\: r = 40\%,\: p_0 = 0.50,\: p_r = 0.05,\: d = 0.99$.

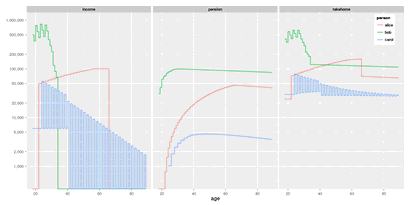
The intent here is that you can build up a pension sufficient for a comfortable retirement either by earning relatively small amounts of money over a long time, or by earning large amounts of money over a relatively short time. That way, the system acts to smooth out the take-home pay of people whose income comes in bursts, which is characteristic of a lot of creative jobs (that people generally prefer over day jobs, if given the choice). Unfortunately this did not work out as well as I was hoping it would; I think the decay mechanism needs to be more sophisticated, possibly with $T$ initially earning interest rather than decaying. But I’ve spent enough time messing with this. More fully baked ideas solicited.

It is probably a good idea for the BLS to phase in starting at age 12 give or take, and it is probably also a good idea to have pension contributions at least partially transfer to one’s heirs upon death (if only to reduce people’s need for life insurance), but I haven’t thought these bits through carefully.

One final consideration is that in the USA, lots of people have tax-advantaged retirement accounts holding much of their savings. It probably makes sense to preserve these, if only to smooth the transition. In keeping with the general no-questions-asked principle behind this proposal, something like this might work: A long-term investment account is defined as a bank or brokerage account intended to accumulate capital over the long term. It must invest the money according to a fixed algorithm (this list of stocks is a valid choice); the algorithm and/or its parameters may be changed no more than once a month, and all earnings from the investments must be reinvested according to the same algorithm. You can stick as much of your pretax income in one of these as you want. If you’re content to live on the BLS despite earning $10,000,000 a year, your tax obligation can be zero. You can also withdraw money from the account whenever you want. Withdrawals count as regular income; there is no calculation of cost basis, length of holding, or anything like that.

If this were actually going to be implemented, existing pension plans would need to be converted to the new system (providing an equivalent benefit at the time of the conversion, ideally), it would need to come along with a sane national health insurance scheme (read single payer of some variety), and it might be a good idea to manipulate the states into scrapping their own income taxes in favor of some sort of share in the national income tax. While we’re at it it would make sense to make property taxes Georgian and replace sales taxes with an at-source carbon tax, but that would be the pony to go along with the impossible wish.

In case anyone wants to play with the numbers, the R script that generated the graphs is available here.